Economic Growth: Solow
A long, long time ago in a galaxy far, far away
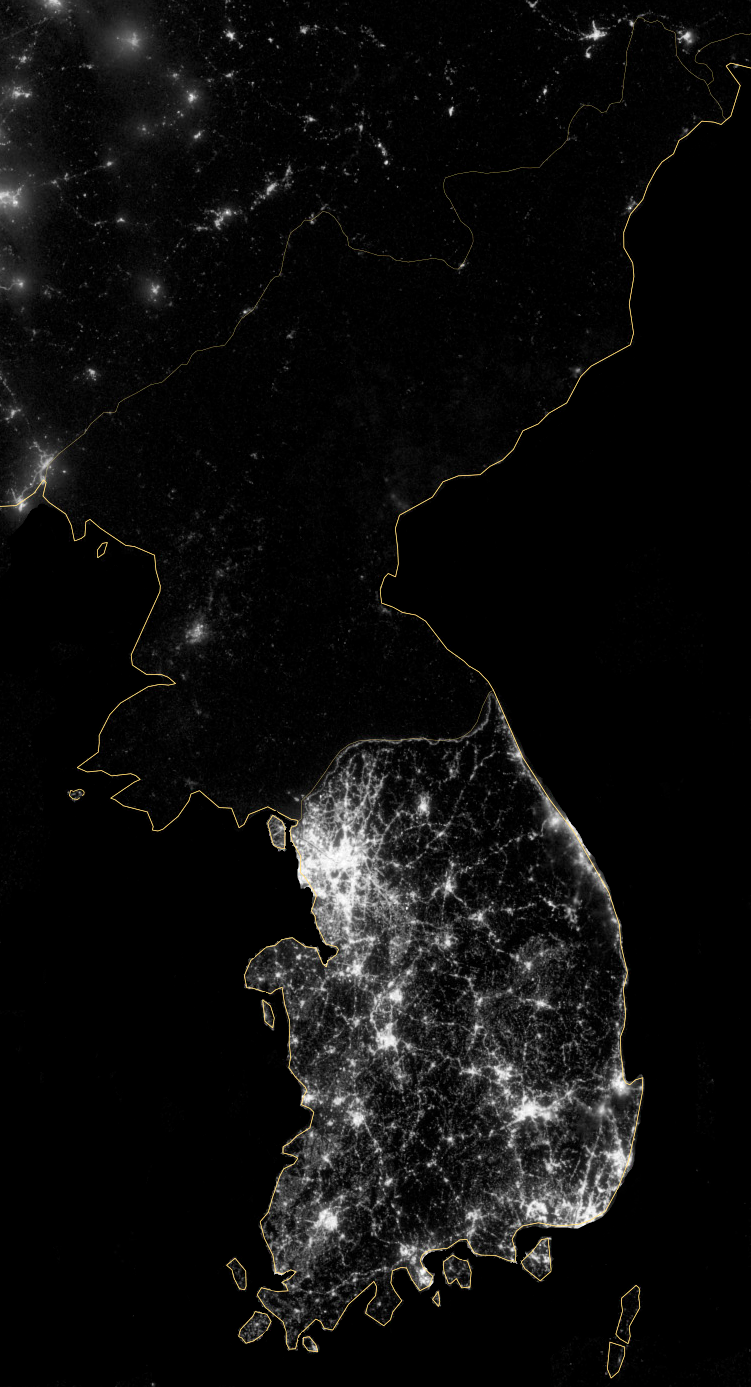
Which country is this?
Life expectancy at birth is under 50 years, and 1 out of every 10 infants die before reaching a first birthday.
More than 90 per cent of households have no electricity, refrigerator, telephone, or car.
Fewer than 10 percent of young adults have graduated from high school.
Is it Kenya, or Bangladesh, or perhaps North Korea?
Non of them.
In fact, the the country is the United States, not today but at the end of the nineteenth century.
Thomas Hobbes: nasty, brutish, and short

Thomas Hobbes:. 1588 - 1679
For most of history, standards of living were extremely low, not much different from that in the poorest countries of the world today.
Evidence suggests, for example, that wages in ancient Greece and Rome were approximately equal to wages in Britain in the century or France in the
In the words of seventeenth-century English philosopher Thomas Hobbes, life was Thomas Hobbes: “solitary, poor, nasty, brutish, and short”
Things that didn’t exist 20 years ago:
iPhone
Facebook
YouTube
Instagram
Twitter
TikTok
Android
Bitcoin
Tesla
iPad
Gmail
WhatsApp
Spotify
Airbnb
Uber
Our lives and habits are completely different than our parents’ generation.
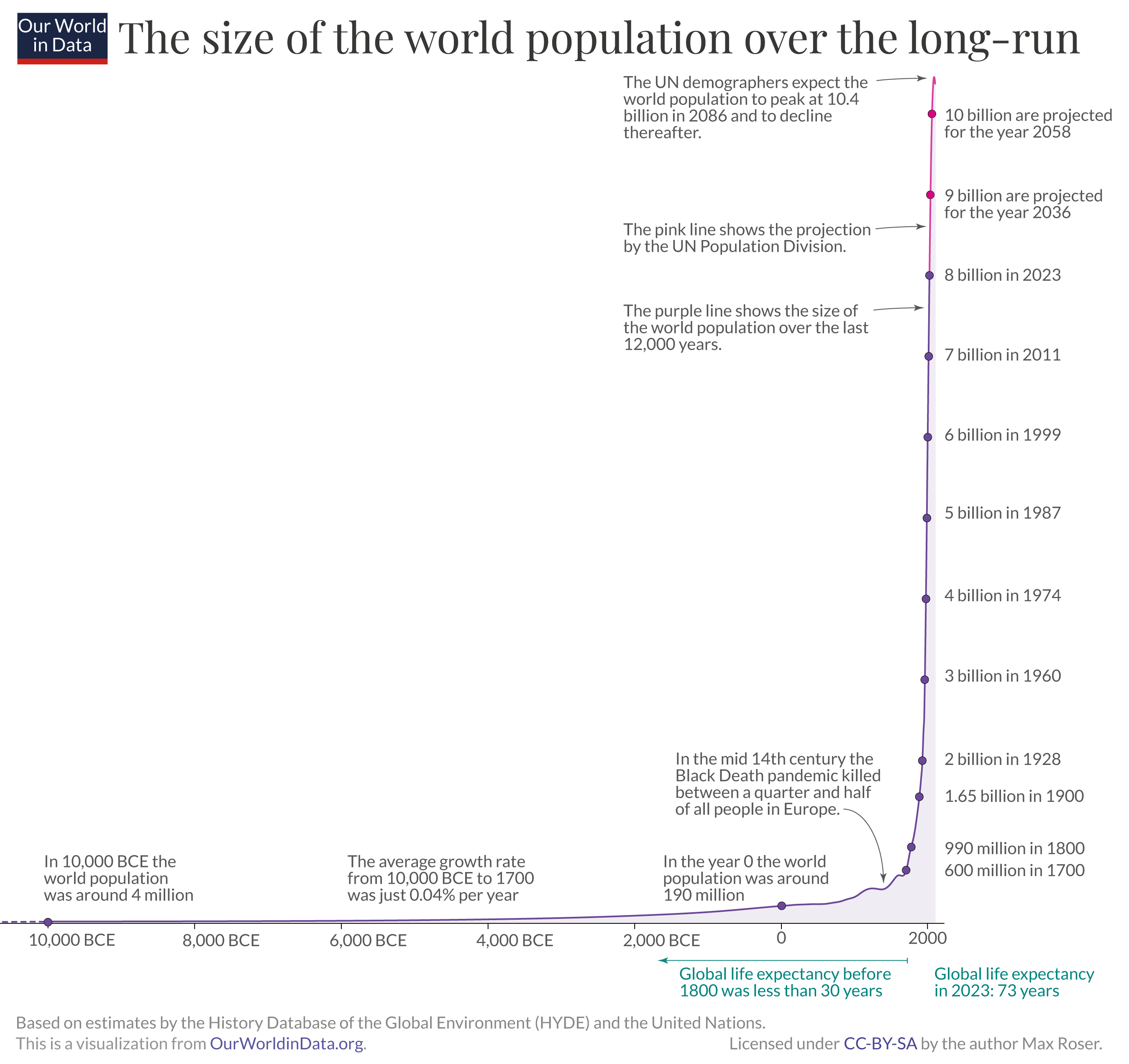
Not just getting richer but getting crowded too: World Population
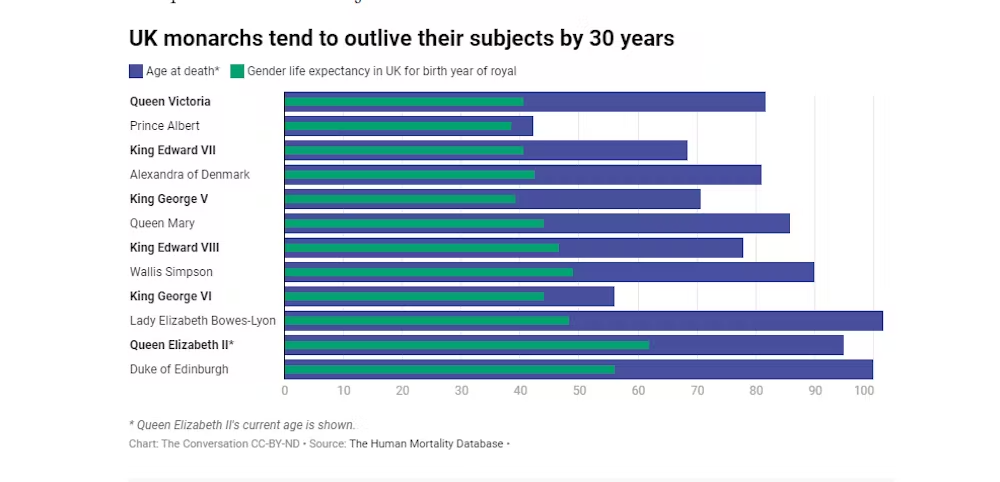
Life expectancy: not as in before
Eat well live long
Richer and Happier
Be happy and live long
Get richer and work less
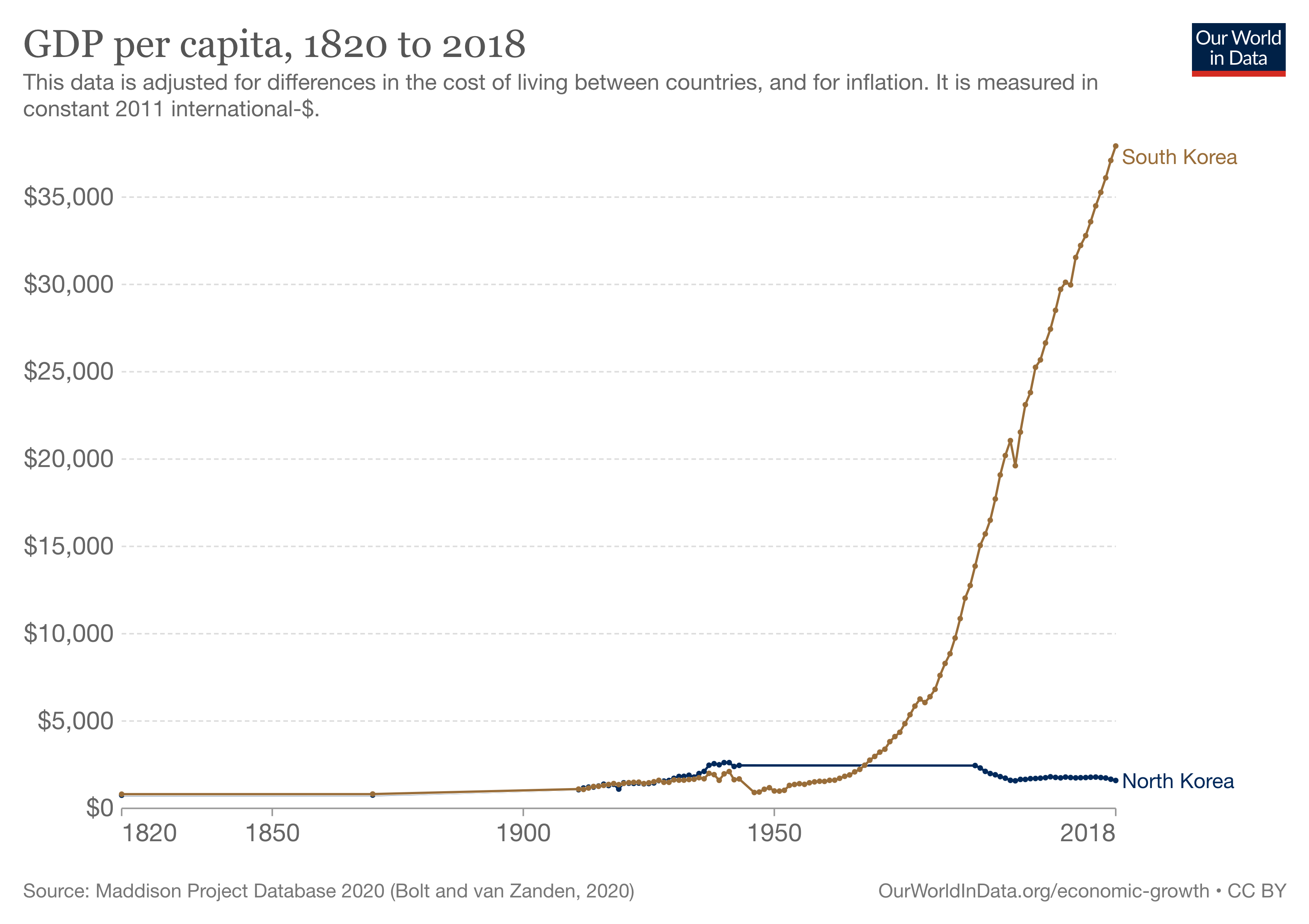
Great Divergence
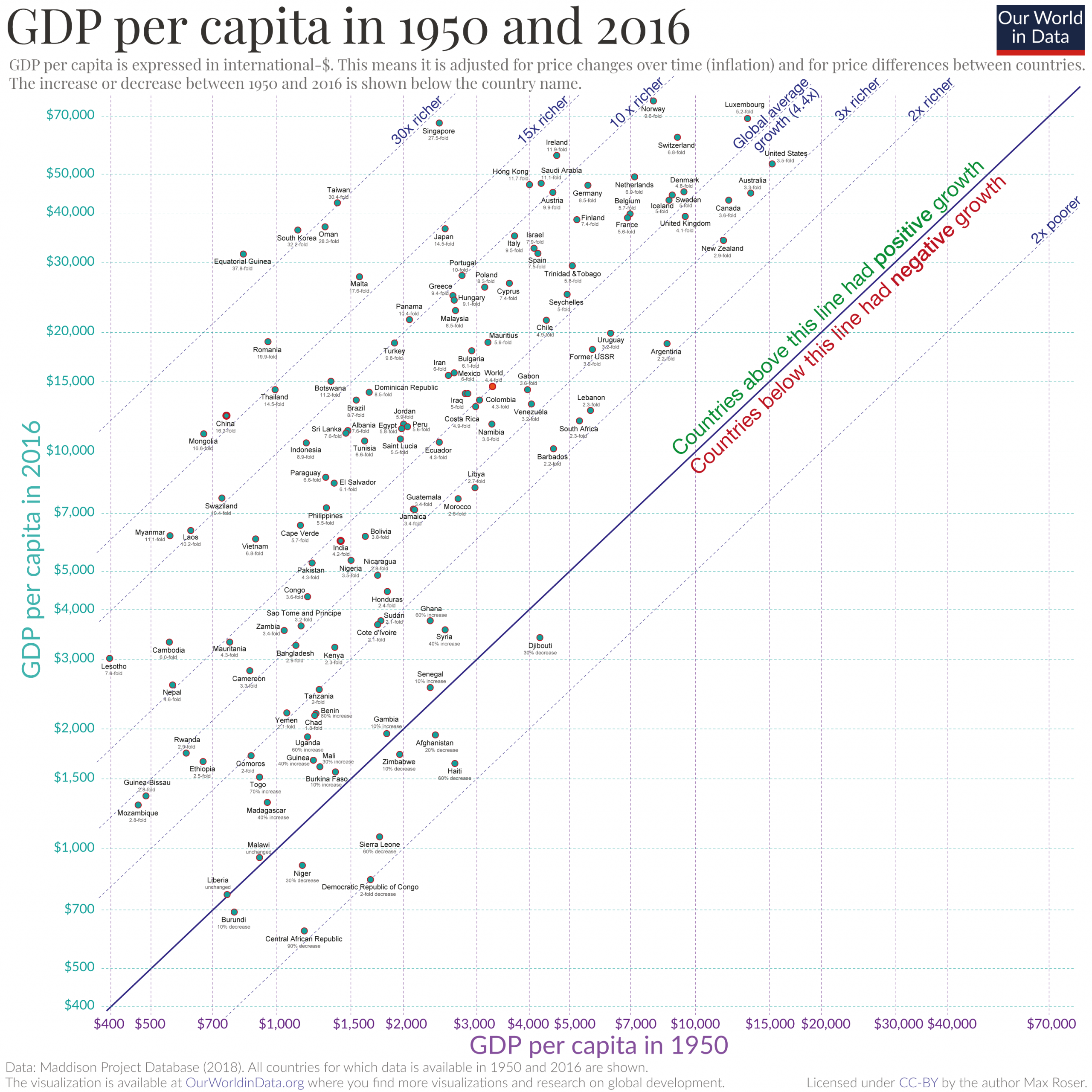
An important result of these differences in timing is that living standards around the world today vary dramatically.
Per capita GDP in Japan and the United Kingdom is about 3/4 that in the United States; for Argentina and China, the ratio is 1/3 or less; and for Ghana, only 1/15.
These differences are especially stunning when we consider that living standards around the world probably differed by no more than a factor of 2 or 3 before the year 1700.
In the past three centuries, standards of living have diverged dramatically, a phenomenon that has been called the Great Divergence.
For example, standards of living in Ghana today are perhaps only five times as high as they were over most of history, and sustained growth is not especially evident.
Global Inequality
Not a One World: Today and Two Hundred Years Ago
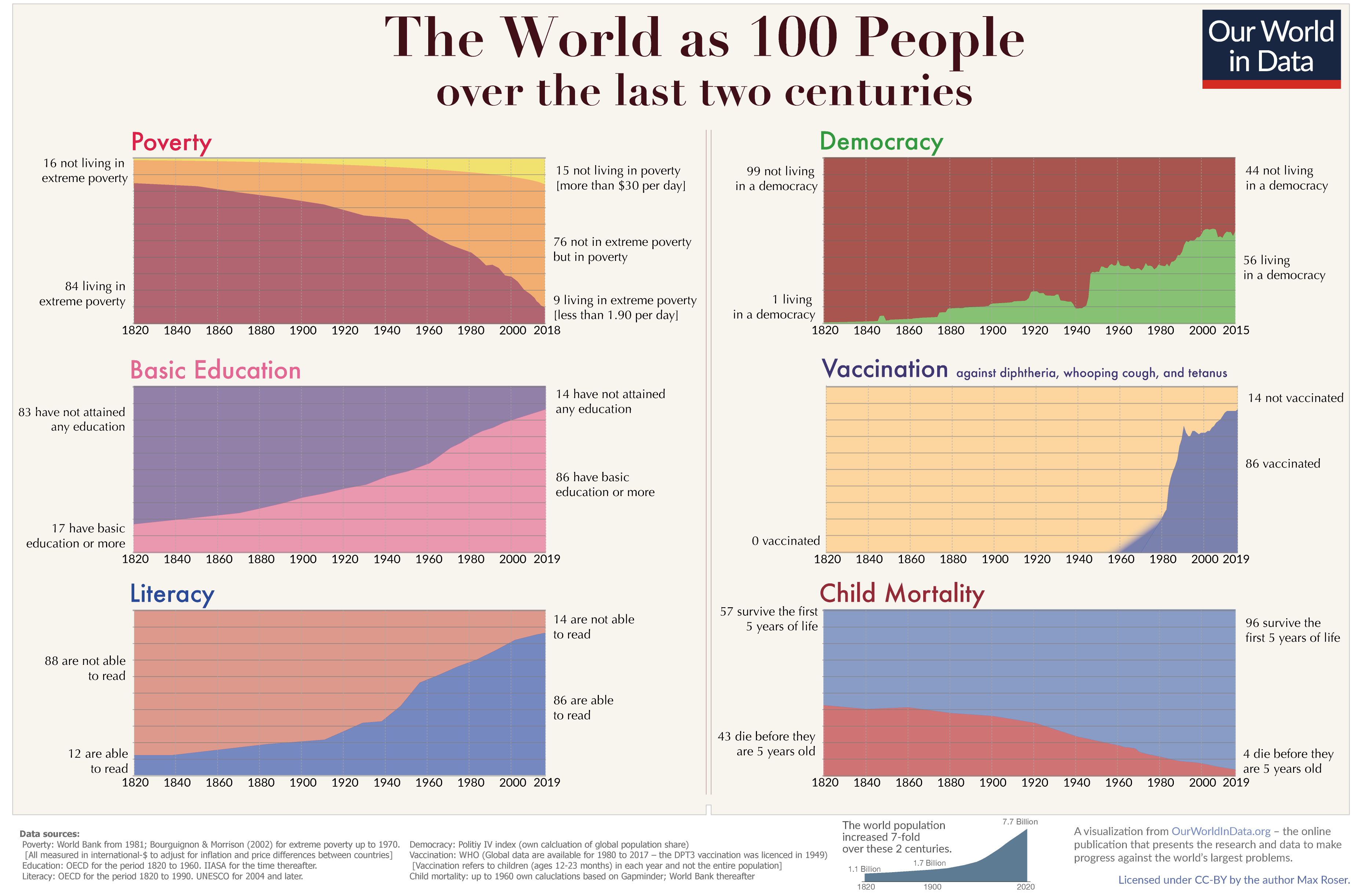
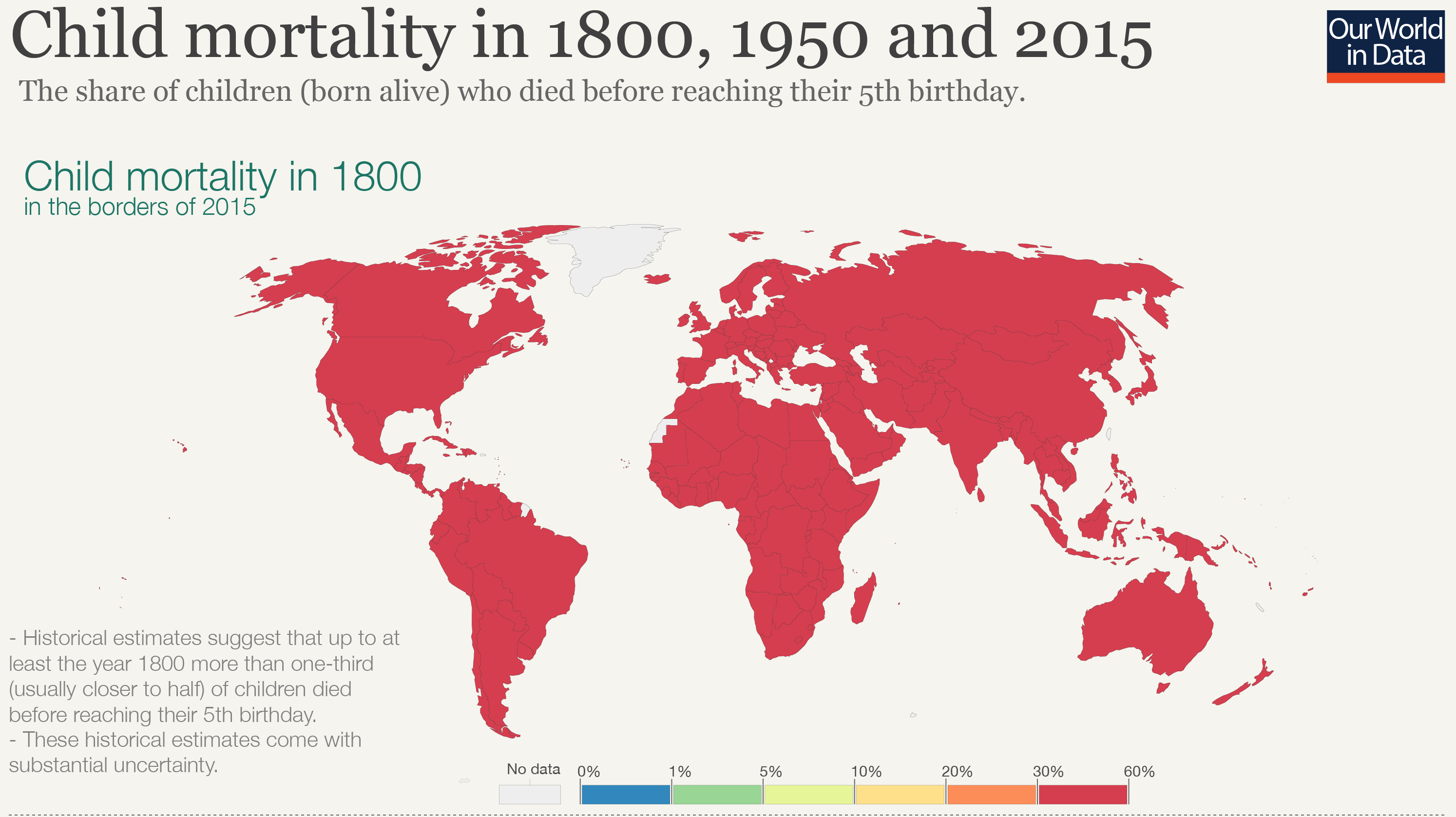
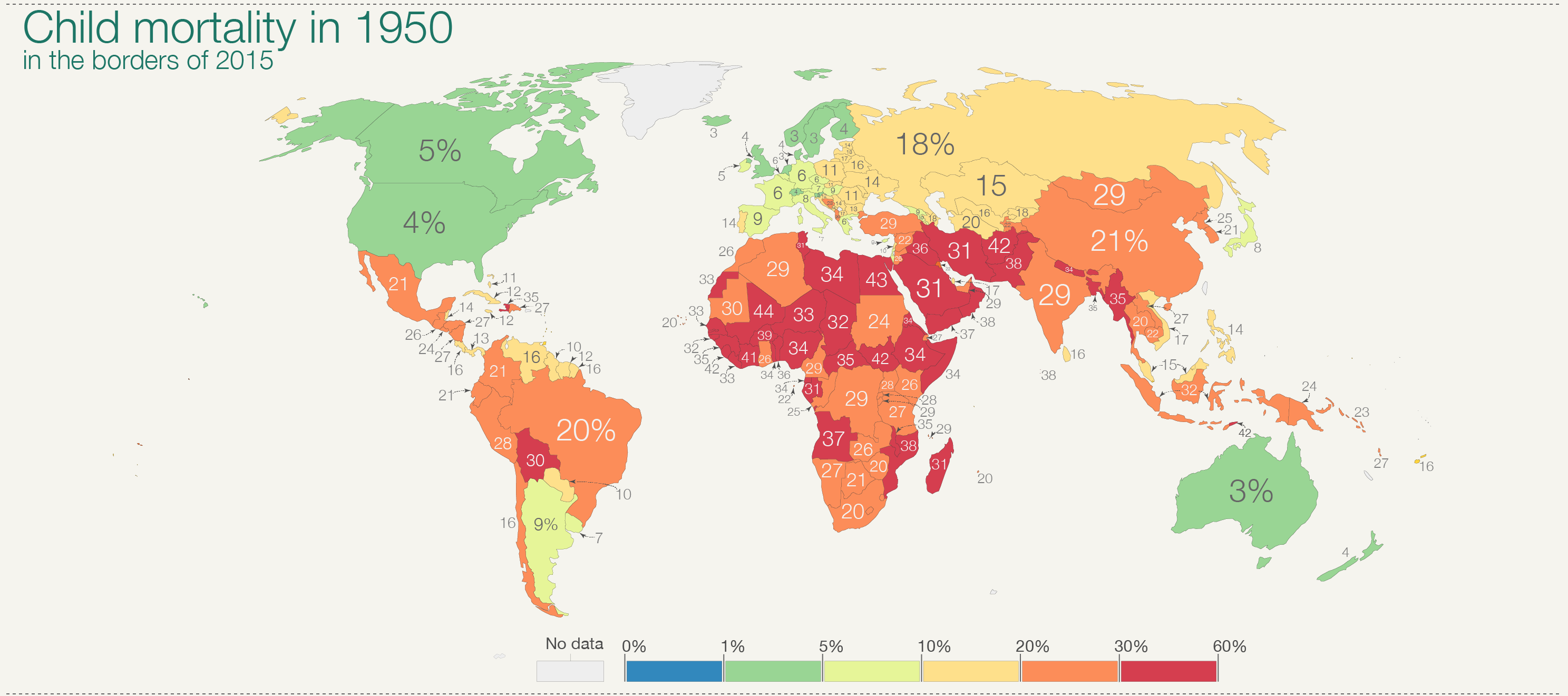
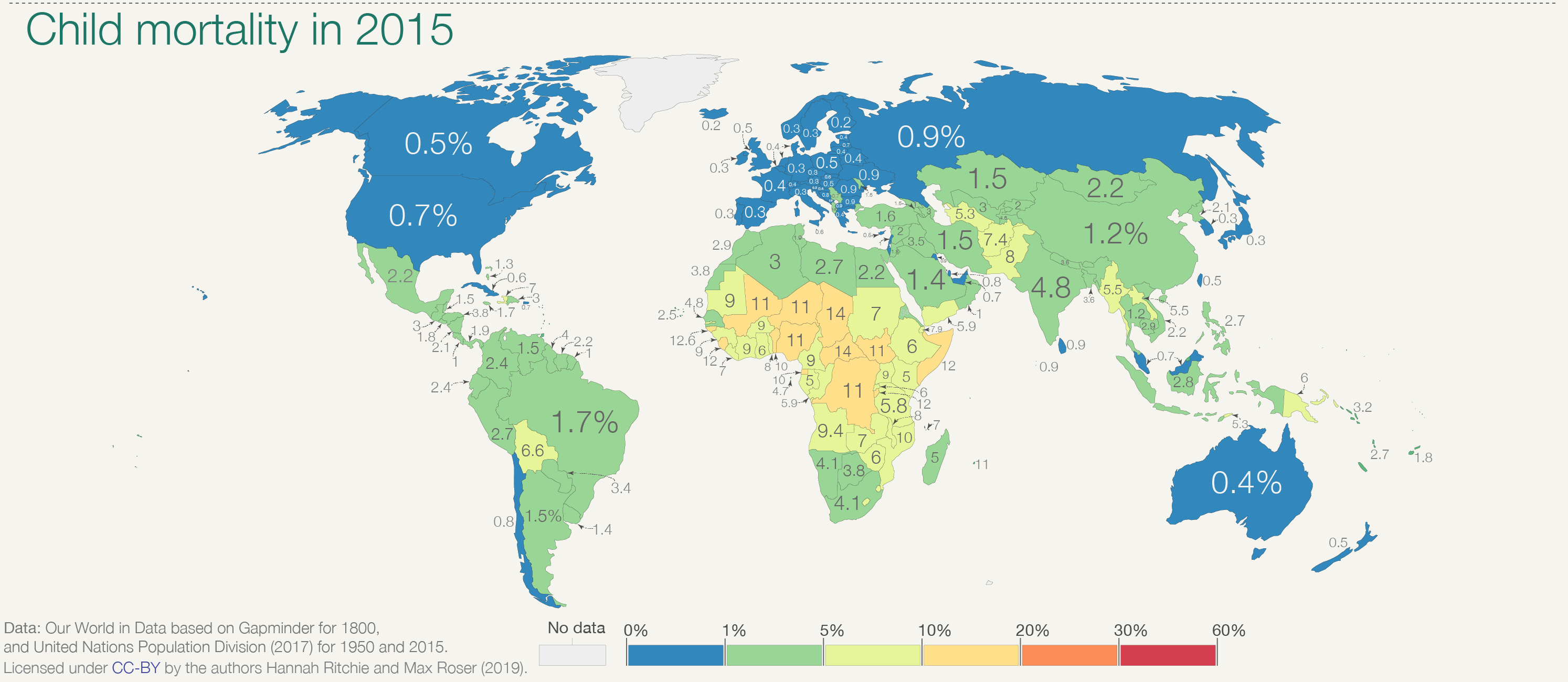
Why?
Democracy ? Not Really
Human Rights
Human Rights and Democracy
GDP and Education
Child Mortality and Women Education
Corruption
Corruption and Education
Human Capital and GDP
Mastering Techniques: Essential Maths for Growth
Growth Rates
Mastering these simple techniques is essential for getting a handle on growth theory and will also come in handy when examining any economic time series data.
- Annual Growth Rate
| Years | Real GDP per capita (2005 US$) | Log of real GDP per capita |
|---|---|---|
| 1950 | 12802 | 9.457 |
| 2010 | 42287 | 10.652 |
| 2011 | 42646 | 10.661 |
What is the US real GDP per capita in 2011?
| Years | Real GDP per capita (2005 US$) | Log of real GDP per capita |
|---|---|---|
| 1950 | 12802 | 9.457 |
| 2010 | 42287 | 10.652 |
| 2011 | 42646 | 10.661 |
\[\gamma_{y} = \frac{y_{t+1} - y_{t}}{y_{t}} \longrightarrow \frac{42646 - 42287}{42287} =0.0085=0.85\%\]
The growth rate of US real GDP per capita in 2011 was \(0.85\%\).
\[\gamma_{y} = \frac{y_{t+1} - y_{t}}{y_{t}} = \frac{y_{t+1}}{y_{t}} - 1 =0.85\%\]
Growth Rates: The Log Difference Method
We are using the log difference method to approximate annual growth rates, as shown by the following formula:
\[\gamma_{y} \approx log(y_{t+1}) - log(y_{t}) \longrightarrow log(42646) - log(42287) =0.85\%\]
The log difference method gives a good approximation of the annual growth rate when growth rates are relatively small for example when
\[log( 1+ \gamma_{y}) \approx \gamma_{y}\]
A Simple Question
| Years | Real GDP per capita (2005 US$) | Log of real GDP per capita |
|---|---|---|
| 1950 | 12802 | 9.457 |
| 2010 | 42287 | 10.652 |
| 2011 | 42646 | 10.661 |
What is the average growth rate between 1950 and 2011?
The compound annual growth rate for discrete time periods is
\[\bar{\gamma_{y}} = \Big( \frac{y_{t}}{y_{0}} \Big)^{1/t} - 1 \quad \longrightarrow \quad y_{t}= y_{0} (1 + \bar{\gamma_{y}})^{t}\]
\[\bar{\gamma_{y}} = \Big( \frac{42646}{12802} \Big)^{1/61} - 1 = 2.4\% \]
The average growth rate of US real GDP per capita between 1950 and 2011 was \(2.4\%\).
Who is this guy?

Luca Paciolis:. 1445–1514
Father of Accounting



Rule of 72 - Rule of 69.3 - - Rule of 70
- The rule of \(72\) is a simple method to determine the amount of time investment would take to double, given a fixed annual interest rate. To use the rule of \(72\), divide \(72\) by the annual rate of return.
\[t=\frac{ln(2)}{ln(1+ r/100)} \approx \frac{72}{r}\]
- The rule of \(70\) is used to determine the number of years it takes for a variable to double/half by dividing the number \(70\) by the variable’s growth/decay rate. The rule of \(70\) is generally used to determine how long it would take for an investment to double/half, given the annual rate of return.
\[ t= \frac{70}{r}\]
Some Useful Properties of Growth Rates Suppose two variables
Suppose two variables \(x\), \(y\), and \(z\) have average annual growth rates of \(g_{x}\), \(g_{y}\), and \(g_{z}\), respectively. Then the following rules apply:
If \(z = x/y\), then \(g_z=g_x - g_y\).
If \(z = x * y\), then \(g_z = g_x + g_y\).
If \(z = x^a\), then \(g_z = a \times g_x\).
If \(z = log(x)\), then \(g_z = 1/x\).
Suppose \(x\) grows at rate \(g_x=0.10\) and \(y\) grows at rate \(g_y=0.03\). What is the growth rate of \(z\) in the following cases?
| \(z=x \times y\) | \(\Rightarrow\) | \(g_z=g_x+g_y=0.13\) |
|---|---|---|
| \(z=x / y\) | \(\Rightarrow\) | \(g_z=g_x-g_y=0.07\) |
| \(z=y / x\) | \(\Rightarrow\) | \(g_z=g_y-g_x=-0.07\) |
| \(z=x^2\) | \(\Rightarrow\) | \(g_z=2 \times g_x=0.20\) |
| \(z=y^{1 / 2}\) | \(\Rightarrow\) | \(g_z=0.5 \times g_y=0.015\) |
| \(z=x^{1 / 2} y^{-1 / 4}\) | \(\Rightarrow\) | \(g_z=0.5 \times g_x-0.25 \times g_y=0.0425\) |
- Source:. Charles Jones, Macroeconomics 2023
Solow Growth Model: An Introduction to Modern Economic Growth Theory
Why Solow Model?

Let use some models with assumptions

Robert M. Solow, Dies at 99 on 21 December 2023

Robert Solow was an intellectual giant - The Economist
Robert M. Solow, Groundbreaking Economist and Nobelist
Solow Model
Capital and Labour
The Solow model presumes that there exists an aggregate production function which maps capital and labour into output.
Labour is denominated in units of time.
Capital refers to
something which must itself be produced,
helps you produce output and
does not get fully used up in the production process.
Capital and labour are both production factors.
They differ in that whereas concept.
Capital and Labour
They also differ in that labour/time is an endowment there is nothing one can do to increase the number of hours available to work in a day.
In contrast, capital can be accumulated.
Furthermore, the amount of hours available tomorrow is independent of how many hours you spend today in other words, how many hours you worked in the past doesn’t influence how many hours you can work in the future. This is the flow feature of labour.
Capital is different in that how much capital you had in the past influences how much capital you’ll have in the future.
This is the stock feature of capital: how much you had in the past influences how much capital you have in the present and future.
Production Function
\(K_{t}\) as the stock of capital in period \(t\).
\(L_{t}\) as the total time spent working in period \(t\). Or simply it is labour.
\(Y_{t}\) denotes output produced in period \(t\).
Suppose that there is a single, representative firm which leases labour and capital from a single, representative household each period to produce output.
The production function is given by
\[\label{eq:productionfunction} Y_{t} = A_{t} F(K_{t}, L_{t})\]
Here \(A_{t}\) is an exogenous variable which measures productivity/technology.
It does not change (for now) and if it does change, it does so permanently. To simplify notation we will drop the \(t\) subscript and simply denote this exogenous variable with \(\textbf{A}\)
Production Function
\(F(\bullet)\) is a function which relates capital and labour into output and has the following properties:
\(F_{K} > 0\) and \(F_{L} > 0\):
The marginal products (of capital or labour) are always positive, so more of either input means more output;
\(F_{KK} < 0\), \(F_{LL} < 0\):
There are diminishing marginal products in both factors, so more of one factor means more output, but the more of the factor you have, the less an additional unit of that factor adds to output;
\(F_{KL} > 0\):
if you have more capital, the marginal product of labour is higher;
\(F(\gamma K_{t}; \gamma L_{t}) = \gamma F (K_{t}; L_{t})\):
the production function has constant returns to scale: If you double both inputs, \(\gamma= 2\), you double output.
Finally, we assume that both capital and labour are necessary to produce, which means that
\(F(0;L_{t}) = F(K_{t};0) = 0\).
An example functional form for \(F(\bullet)\) which we will use throughout the course is the Cobb-Douglas production function:
\[F(K_{t}, L_{t}) = K^{\alpha}_{t} L^{1-\alpha}_{t}, \quad with \quad 0<\alpha<1 \tag{2.1}\]
Let’s verify that this production function (Equation eq-cobbdouglass) satisfies the properties laid out above.
- Since \(0 < \alpha < 1\), and \(K_{t}\) and \(L_{t}\) can’t be negative, the marginal products of capital and labour are both positive.
\[\begin{aligned} F_{K} (K_{t}, L_{t}) &= \alpha K^{\alpha-1}_{t} L^{1-\alpha}_{t} \\ F_{L} (K_{t}, L_{t}) &= (1-\alpha) K^{\alpha}_{t} L^{-\alpha}_{t} \end{aligned}\]
- Again, since \(0 < \alpha < 1\), \(F_{KK}\) and \(F_{LL}\) are both negative, while \(F_{KL} > 0\).
\[\begin{aligned} F_{KK} (K_{t}, L_{t}) &= \alpha (\alpha-1) K^{\alpha-2}_{t} L^{1-\alpha}_{t} \\ F_{LL} (K_{t}, L_{t}) &= - \alpha (1-\alpha) K^{\alpha}_{t} L^{-\alpha-1}_{t} \\ F_{KL} (K_{t}, L_{t}) &= (1- \alpha) \alpha K^{\alpha-1}_{t} L^{-\alpha}_{t} \end{aligned}\]
- Now, let’s verify the constant returns to scale assumption.
\[\begin{aligned} F(\gamma K_{t}, \gamma L_{t}) &= (\gamma K_{t})^{\alpha} (\gamma L_{t})^{1-\alpha} \\ &= \gamma^{\alpha} K_{t}^{\alpha} \gamma^{1-\alpha} L_{t}^{1-\alpha} \\ &= \gamma K_{t}^{\alpha} L_{t}^{1-\alpha} \end{aligned}\]
- Finally, let’s verify that both inputs are necessary for any output to be produced:
\[\begin{aligned} F(0, L_{t}) &= 0^{\alpha} L^{1-\alpha}_{t} \\ F(K_{t},0) &= K^{\alpha}_{t} 0^{\alpha} \end{aligned}\]
As long as \(\alpha \neq 1\) or \(\alpha \neq 0\) both inputs are necessary for production.
Maximisation
The marginal product of capital (MPK) is the increase in output (or the marginal product) resulting from a one unit increase in the capital input, holding all other inputs constant. It measures the additional output produced by an additional unit of capital, and can be used to determine the optimal level of capital to employ in production. The MPK is typically positive at low levels of capital, but may eventually decrease as more capital is added, due to diminishing returns to capita
The marginal product of labor (MPL) is the additional output that is produced by adding one more unit of labor to the production process, holding all other factors of production constant. It represents the increase in total output that results from the hiring of one more worker. The MPL is important for businesses because it helps them to determine the optimal level of labor input to use in their production process in order to maximize profits.
As you might remember from term 1, the optimisation problem of the firm is to choose capital and labour so as to maximise the differences between revenue and total costs or more simply, maximise profit, \(\Pi_{t}\)
\[\max_{\{K_{t},L_{t}\}} \Pi_{t} = A F(K_{t}, L_{t}) - w_{t} L_{t} - R_{t}K_{t}\]
where \(w_{t}\) denotes the real wage paid to labour and \(R_{t}\) denotes the real return to capital. The first order conditions for the representative firm are:
\[\label{eq:wage} w_{t} = A F_{L} (K_{t}, L_{t})\]
\[\label{eq:returnofcapital} R_{t} = A F_{K} (K_{t}, L_{t})\]
These conditions say that the firm ought to hire capital and labour up to until the point at which the marginal benefit of doing so (the marginal product of capital or labour) equals the marginal costs of doing so (the factor price).
Total Expenditure and Total Output
The representative household is endowed with labour(time) \(L_{t}\)
Initial stock of capital, \(K_{t}\)
Household earns income from supplying capital and labour to the firm \(w_{t}L_{t} + R_{t}K_{t}\)
Household can consume its income, \(C_{t}\), or invest some of it in additional capital, \(I_{t}\)
Thus, household budget constraint becomes:
\[C_{t} + I_{t} \leq w_{t}L_{t} + R_{t}K_{t} \tag{2.2}\]
- Equation eq-budgetconst says that total expenditure equals total income which equals the total output. In other words:
\[ Y_{t} = C_{t} + I_{t} \tag{2.3}\]
Capital Accumulation Equation: Central Equation of Solow Model
We know today’s capital stock but we do not know tomorrow’s level of capital which is the main question of economic growth.
In other words, the initial level of capital, \(K_{t}\), is given and future levels of capital, \(K_{t+1}\) is the question and can be influenced through investment.
Investment in period \(t\) yields new capital in period \(t+1\)
As expected, some existing capital will depreciate during production.
Formally, capital accumulates according to:
\[ K_{t+1} = I_{t} + (1-\delta ) K_{t} \tag{2.4}\]
\[ K_{t+1} = I_{t} + (1-\delta ) K_{t} \tag{2.5}\]
Where \(0 < \delta < 1\) is the depreciation rate (the fraction of the capital stock that goes bad or becomes obsolete each period).
The Equation eq-aggregate_capital_accumulation is one of the most important equations in the Solow model. It is known as the capital accumulation equation or a law of motion for capital.
Equation eq-aggregate_capital_accumulationss says that your tomorrow (\(t+1\)) capital stock equals your investment in today (\(t\)) plus the non-depreciated stock of capital with which you started.
Investment in Solow Model
The Solow model assumes that investment is a constant fraction of output.
Let say \(s\) is the saving rate, –equivalently, the investment rate– and \(0<s<1\)
\[I_{t} = sY_{t} \tag{2.6}\]
Combining Equation eq-investmentrate and Equation eq-output_expenditure implies:
\[ C_{t}=(1-s)Y_{t} \tag{2.7}\]
- The Solow model is therefore assuming that the economy as a whole consumes a constant fraction of its output each period, investing the other fraction.
All Together: Aggregate Level
Putting all of this together, the Solow model is characterized by the following equations all simultaneously holding:
\[ Y_{t} = A F(K_{t}, L_{t}) \tag{2.8}\]
\[ Y_{t} = C_{t} + I_{t} \]
\[ K_{t+1} = I_{t} + (1-\delta ) K_{t} \tag{2.9}\]
\[ I_{t} = sY_{t} \tag{2.10}\]
\[ w_{t} = A F_{L}(K_{t}, L_{t}) \]
\[ R_{t} = A F_{K}(K_{t}, L_{t}) \]
This is six equations and six endogenous variables, \(Y_{t}\), \(C_{t}\), \(I_{t}\), \(K_{t+1}\), \(w_{t}\), and \(R_{t}\).
\(L_{t}\), \(K_{t}\), and \(A\) are exogenous variables (taken as given).
\(s\) and \(\delta\) are parameters.
Central Equation
Equation eq-output, Equation eq-capital_accu, and Equation eq-investmentx can be combine into one central equation describing the evolution of capital over time.
\[ K_{t+1} = sAF(K_{t}, L_{t}) + (1-\delta ) K_{t} \tag{2.11}\]
This equation describes the evolution of \(K_{t}\).
Given an exogenous current value of \(K_{t}\), it tells you how much \(K_{t+1}\) an economy will have, given exogenous values for \(A\) and \(N_{t}\), and values for the parameters \(s\) and \(\delta\)
It is helpful to write this in terms of capital per worker. Thus divide both side of Equation eq-11 by \(L_{t}\):
\[\frac{K_{t+1}}{L_{t}} = \frac{sAF(K_{t}, L_{t})}{L_{t}} + (1- \delta)\frac{K_{t}}{L_{t}} \tag{2.12}\]
Let’s define capital per worker - or capital per capital
\[k_{t} \equiv \frac{K_{t}}{L_{t}}\]
- Using the properties of the production function, in particular the assumption that it is constant returns to scale, we can write:
\[\frac{F(K_{t}, L_{t})}{L_{t}} = F\Big(\frac{K_{t}}{L_{t}} \Big) = F(k_{t},1)\]
- Therefore, we will use \(f(k_{t})\equiv F(k_{t},1)\) as the per worker production function. Thus, we can re-write the central equation ((eq?)-) as:
\[\frac{K_{t+1}}{L_{t}} = sAf(k_{t}) + (1- \delta) k_{t}\]
- Multiply and divide the left-hand side by \(L_{t+1}\) and re-arranging terms so as to write it in terms of capital per worker
\[\frac{K_{t+1}}{L_{t}} \frac{L_{t+1}}{L_{t+1}}= sAf(k_{t}) + (1- \delta) k_{t}\]
- Since we are assuming that labour is constant across time, this means that \(L_{t+1} / L_{t} = 1\) So we can write:
\[ k_{t+1} = sAf(k_{t}) + (1- \delta) k_{t} \tag{2.13}\]
Equation eq-capitalperworker is the central equation of the Solow model.
It describes how capital per worker evolves over time, given an initial value of the capital stock, an exogenous value of \(A\), and parameter values \(s\) and \(\delta\)
All Together: Capital Per Worker Level
- We can define \(y_{t}\), \(c_{t}\), and \(i_{t}\) as output, consumption, and investment per worker. An again \(k_{t}\) capital per worker. Thus, in terms of \(k_{t}\), we can re-write equations in Page: 58 Aggregate Level
\[\begin{aligned}{5} y_{t} & = A f(k_{t}) \label{eq-output2} \\ c_{t} & = (1-s)A f(k_{t}) \\ i_{t} & = s A f(k_{t}) \\ w_{t}& = A f'(k_{t}) \\ R_{t} & = A f(k_{t}) - k_{t} A f'(k_{t}) \end{aligned}\]
- Suppose that we have the Cobb-Douglas production function. The central equation of the Solow model Equation eq-capitalperworker can be written:
\[k_{t+1} = sAf(k^{\alpha}_{t}) + (1- \delta) k_{t}\]
- The other variables are determined as a function of \(k_{t}\). These can be written:
\[\begin{aligned} y_{t} & = A k^{\alpha}_{t} \label{eq-output2c} \\ c_{t} & = (1-s)A k^{\alpha}_{t} \\ i_{t} & = s A k^{\alpha}_{t} \\ w_{t}& = (1-\alpha) A k^{\alpha}_{t} \\ R_{t} & = \alpha A k^{\alpha-1}_{t} \end{aligned}\]
