Week 6 Problem Set
Question 1:
Getting to know the Shapiro-Stiglitz model [Romer 11.3]
Describe how each of the following affects equilibrium employment and the wage in the Shapiro Stiglitz model:
a) An increase in workers’ discount rate, \rho.
b) An increase in the job breakup rate, b.
c) A positive multiplicative shock to the production function (that is, suppose the production function is AF(L), and consider an increase in A).
d) An increase in the size of the labour force, \bar{L}.
Provide economic intuition for each result.
Question 2:
To let shirk or not to let shirk?
This question asks about a highly simplified version of the Shapiro-Stiglitz shirking model covered in the lecture. We are interested in whether it makes sense for a firm to monitor its workers and pay wages sufficiently high to prevent shirking. The problem was trivial in the lecture because shirking workers were assumed to be completely unproductive. To make the problem interesting we therefore assume that even workers who shirk and exert zero effort have some productivity. In particular, we assume that shirking workers have productivity 1 and non-shirking workers have productivity x > 1, so the firm receives revenue 1 per worker if the worker shirks and revenue x if the worker does not shirk. Monitoring is assumed to have unit cost, so the expected cost of monitoring at the rate q is simply q. The expected profit (per worker) of a firm monitoring at the rate q and paying wage w is therefore:
\pi = R - w - q
where R = x if the worker exerts effort \bar{e} and R=1 if the worker shirks and exerts no effort.
Building on the results we derived in the lecture, assume that to induce effort \bar{e}, the firm must pay the no-shirking wage:
w = \bar{e} + \mu\frac{\bar{e}}{q}
i.e. compensate the cost of effort \bar{e} plus pay a premium of \mu\frac{\bar{e}}{q}. \mu here is a function of workers’ preferences and aggregate macroeconomic conditions that the firm takes as given when setting its own wage and the rate of monitoring q. Assume also that a worker who is shirking and exerting zero effort is willing to take up the job at any non-negative wage.
a) Suppose the firm decides not to bother satisfying the non-shirking condition and simply lives with shirking workers. What monitoring probability will the firm set if they maximise expected profit? What wage will it pay? What will be its profits?
b) Suppose the firm now decides to set the monitoring probability and wage to induce its workers not to shirk. Set up an optimisation problem for the firm to determine the optimal monitoring rate q^* and optimal wage w^* to prevent shirking. Discuss how and why these variables depend on the primitives of the model. Based on the lecture, what factors can affect \mu, and how do changes in \mu affect the firm’s choices?
c) Show that there will be no shirking in this economy iff
x - \bar{e} - 2\sqrt{\mu \bar{e}} > 1
Interpret.
Question 3:
The fair wage-effort hypothesis (Akerlof and Yellen, 1990) [Romer 11.5]
Preamble: This problem introduces you to the fair wage-effort hypothesis, which is another efficiency wage theory, and a nice alternative to the Shapiro-Stiglitz model covered in the lecture. The maths here is very simple, but if you get stuck, there will be solutions next week, with a little bonus 😊
Suppose there are a large number of firms, N, each with profits given by F (eL) - wL, F'(\cdot) > 0, F''(\cdot) < 0. L is the number of workers the firm hires, w is the wage it pays, and e is workers’ effort. Effort is given by e = \min[w/w^*,1], where w^* is the “fair wage”; that is, if workers are paid less than the fair wage, they reduce their effort in proportion to the shortfall.
Akerlof and Yellen motivate the fair wage-effort hypothesis by an observation that human behaviour is strongly driven by the sense of fairness and equity: when employees do not get what they think they deserve, they try to get even at their employers.
This theory has strong grounding in psychology, sociology, and is considered obvious in HR textbooks. You are invited to investigate its macroeconomic implications.
Assume that there are \bar{L} workers who are willing to work at any positive wage.
a) If a firm can hire workers at any wage, what value (or range of values) of w minimizes the cost per unit of effective labour, w/e? For the remainder of the problem, assume that if the firm is indifferent over a range of possible wages, it pays the highest value in this range.
b) Suppose w^* is given by w^* = \bar{w} +a -bu, where u is the unemployment rate and \bar{w} is the average wage paid by the firms in the economy. Assume b > 0 and a/b < 1.
i. Given your answer to part (a) (and the assumption about what firms pay in cases of indifference), what wage does the representative firm pay if it can choose w freely (taking \bar{w} and u as given)?
ii. Under what conditions does the equilibrium involve positive unemployment and no constraints on firms’ choice of w? (Hint: In this case, equilibrium requires that the representative firm, taking \bar{w} as given, wishes to pay \bar{w}.) What is the unemployment rate in this case?
iii. Under what conditions is there full employment?
c) Suppose there are two types of workers: high-productivity and low-productivity. The representative firm’s production function is modified to be F (Ae_1L_1 + e_2L_2), A >1, where L_1 and L_2 are the numbers of high-productivity and low-productivity workers the firm hires.
Assume that e_i = \min[w_i/w^*_i,1], where w^*_i is the fair wage for type-i workers. w^*_i is given by w^*_i = [(\bar{w}_1 +\bar{w}_2)/2]-bu_i , where b > 0, \bar{w}_i is the average wage paid to workers of type i , and u_i is their unemployment rate. Therefore, the fair wage for each type partly depends on the wages received by other members of the workforce.1 Finally, assume there are \bar{L} workers of each type.
i. Explain why, given your answer to part (a) (and the assumption about what firms pay in cases of indifference), neither type of worker will be paid less than the fair wage for that type.
ii. Explain why w_1 will exceed w_2 by a factor of A.
iii. In equilibrium, is there unemployment among high-productivity workers? Explain. (Hint: If u_1 is positive, firms are unconstrained in their choice of w_1.)
iv. In equilibrium, is there unemployment among low-productivity workers? Explain.
Question 4:
Getting to know the Search and Matching model
Consider the Diamond-Mortensen-Pissarides model (Diamond, 1982; Mortensen & Pissarides, 1994; Pissarides, 2000) studied in the lecture.
Describe how each of the following affects steady-state (un)employment and output:
An increase in unemployment benefits, **b**.
A decrease in the matching efficiency, **e**.
An increase in the productivity, **z**.
Provide economic intuition with analytical mechanisms for each result.
Question 5:
The Beveridge curve in recent years
Interpret the different patterns observed in terms of the Diamond-Mortensen-Pissarides search and matching model studied in the lectures. Carefully provide the intuition and describe any relationships you use.
Here’s the text converted to markdown format:
Figure [fig:beveridge_curve] plots vacancies against unemployment in the US for December 2000 - December 2024. However, when I have split the Beveridge‐curve data into multiple time periods and fit separate trend lines for each, as shown in Figure [fig:beveridge_curve_trends], I get different slopes for the trend lines. Why do the trend lines have different slopes? What economic factors might explain these varying slopes?
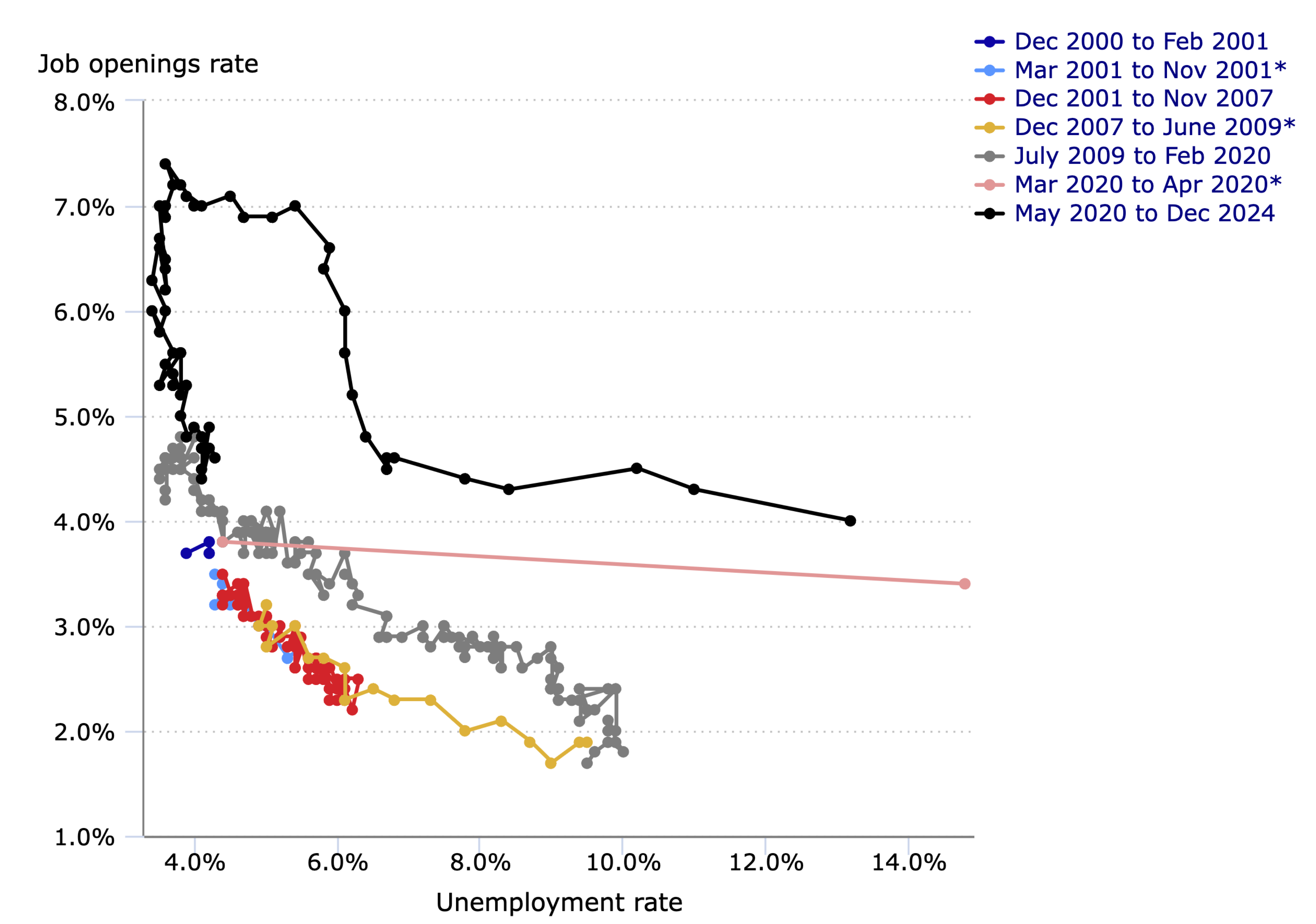
The Beveridge curve in the US, December 2000 - December 2024
Source: US Bureau of Labour Statistics. * Represents recession, as determined by NBER
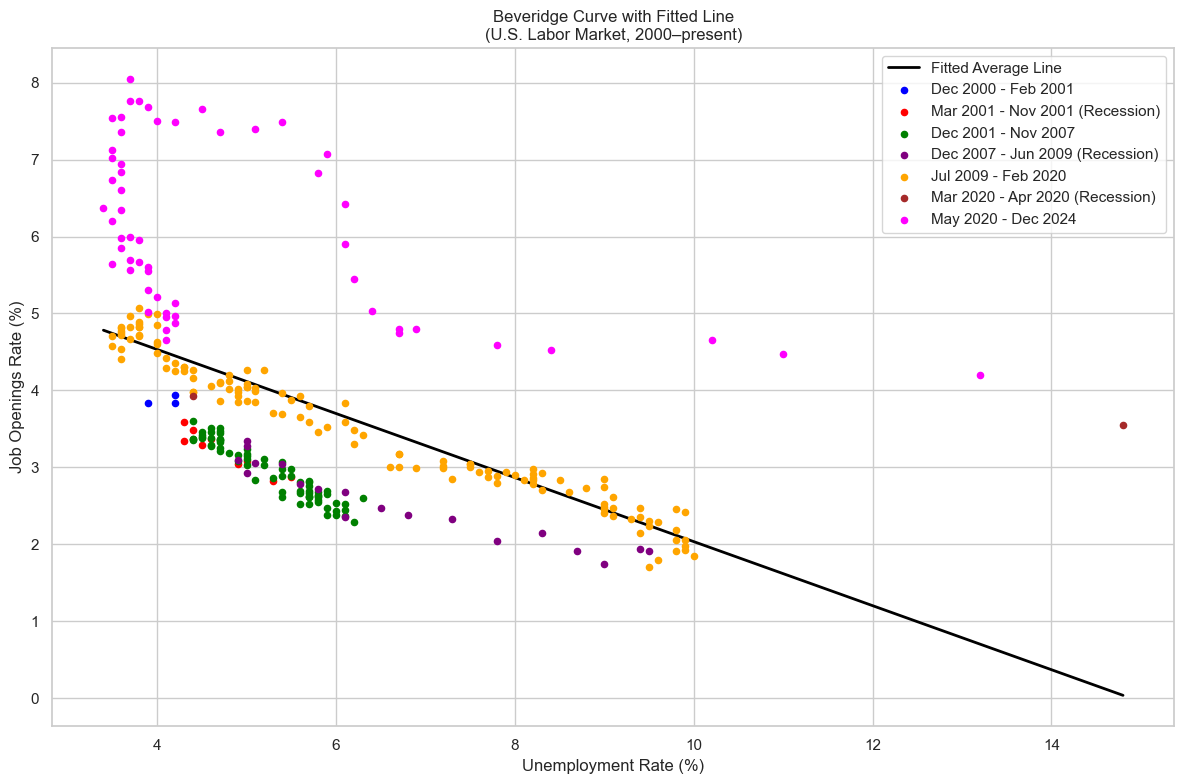Fitted line for the period 2000-2024
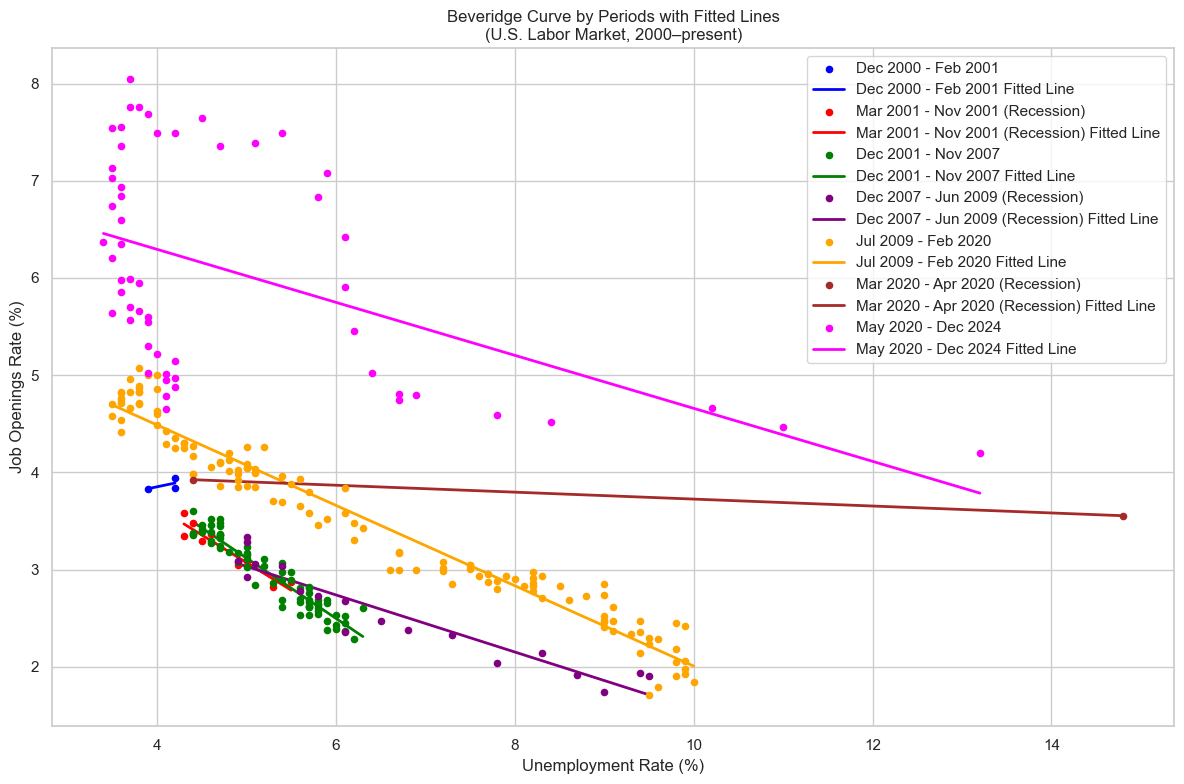Different fitted lines for different periods
Notes & Source: Data: US Bureau of Labour Statistics. Calculations: Fatih Kansoy.
We assume a simple average of the mean wages in the two groups for simplicity only, and this can be relaxed.↩︎